1.3 Упругие волны в сплошной среде
Механические
возмущения, распространяющиеся в упругой среде с конечной скоростью,
называются упругими или механическими
волнами. Тела, которые, воздействуя на упругую среду, вызывают эти
возмущения, называют источниками упругих волн.
Упругая волна является продольной, если частицы среды колеблются в направлении распространения волны.

Упругая волна является поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны.

В
жидкостях и газах упругие волны всегда продольные. В твердых телах могут
распространяться и продольные, и поперечные волны.
Распространение
в упругой среде механических возмущений, возбуждаемых источником волн, связано с
переносом энергии. Поэтому такие волны
называются бегущими волнами. Скорость
распространения возмущений в среде v называется скоростью
волны (фазовой скоростью). Скорость распространения
упругих волн зависит от плотности и упругих свойств среды.
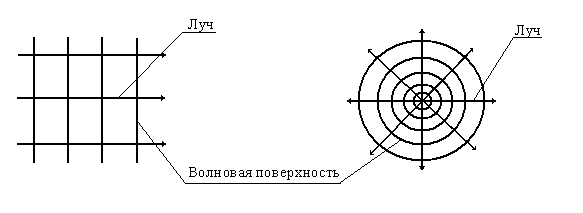
Линия, касательная к которой в каждой ее точке совпадает с направлением распространения волны, называется лучом. Геометрическое место точек, в которых фаза колебаний частиц среды имеет одно и то же значение, называется волновой поверхностью. В однородной среде волновые поверхности перпендикулярны лучам. В зависимости от формы волновых поверхностей различают плоские, сферические, цилиндрические и другие волны. На рисунке представлены плоская и сферическая волны.
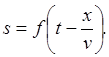
Если
волна распространяется в отрицательном направлении
оси Ox,
то:
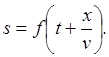
Если
колебания частиц в волне гармонические, то волна
называется гармонической или монохроматической. Уравнение
плоской гармонической волны, бегущей вдоль оси Ox, может быть записано в
виде:
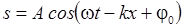 .
.
Здесь A – амплитуда колебаний в
волне, 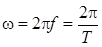 -
циклическая частота волны,
-
циклическая частота волны, 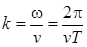 -
волновое число,
-
волновое число, 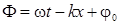 -
фаза волны.
-
фаза волны.
Расстояние,
на которое распространяется волна за время, равное периоду колебаний,
называется длиной волны λ
(м):
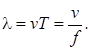
С
учетом этого волновое число можно представить в
виде:
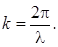
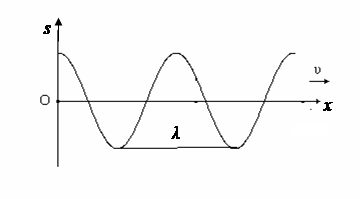
График
зависимости s(x) в
плоской гармонической волне для некоторого момента
времени t представлен на
рисунке:
В
случае, когда плоская волна распространяется в произвольном направлении, ее
уравнение имеет вид:
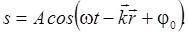
Здесь 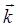 -
волновой вектор. Его модуль равен волновому
числу k, а
направление совпадает с направлением распространения волны в точке с
радиус-вектором
-
волновой вектор. Его модуль равен волновому
числу k, а
направление совпадает с направлением распространения волны в точке с
радиус-вектором 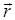 .
.
Экспоненциальная
форма записи уравнения плоской волны:
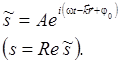
Уравнение
расходящейся сферической волны:
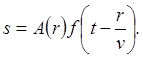
В
случае монохроматической сферической волны:
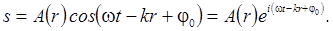
Дифференциальное
уравнение, описывающее распространение волн в однородной изотропной
непоглощающей среде со скоростью v, называется волновым
уравнением и имеет вид:
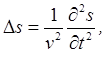
где 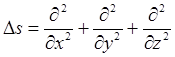 -
оператор Лапласа.
-
оператор Лапласа.
Если
волна гармоническая, то 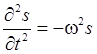 ,
и волновое уравнение принимает вид:
,
и волновое уравнение принимает вид:
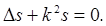
Это
уравнение называется уравнением
Гельмгольца.
Амплитуда, начальная фаза и частота волны определяются колебаниями в источнике волн. Фазовая скорость волны, как уже было сказано выше, зависит от физических свойств среды, в которой распространяется волна.