Физические основы строительной акустики

Периодические колебания называются гармоническими, если колеблющаяся величина меняется с течением времени по закону косинуса или синуса:

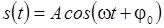
или

.

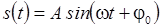Здесь 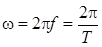 - циклическая частота колебаний, A – максимальное отклонение колеблющейся величины от положения равновесия (амплитуда колебаний), φ(t) = ωt+φ₀ – фаза колебаний, φ₀ – начальная фаза.

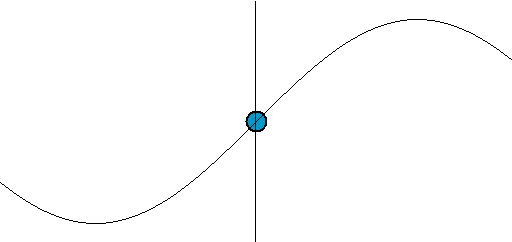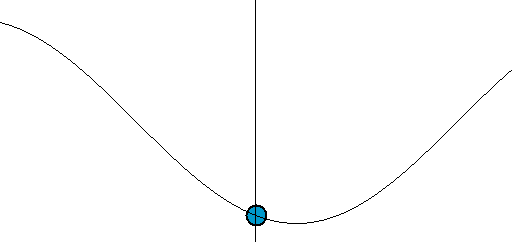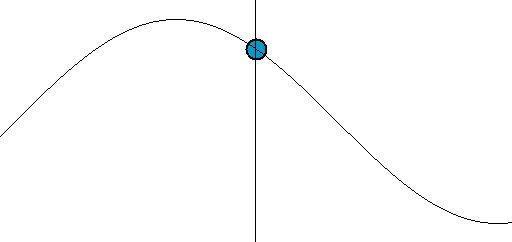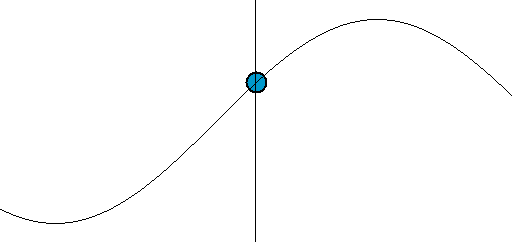
График гармонических колебаний представлен на рисунке:

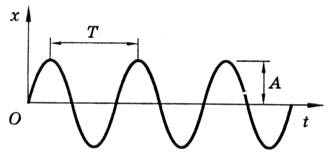
Используя теорему Эйлера (раздел 1.1), можно представить уравнение гармонических колебаний в экспоненциальной форме:

.

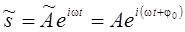
Физический смысл имеет только действительная часть выражения:

.

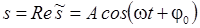На представлении колеблющейся величины в экспоненциальной форме основан способ изображения гармонического колебания в виде векторной диаграммы.  

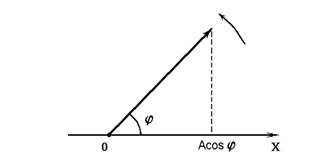
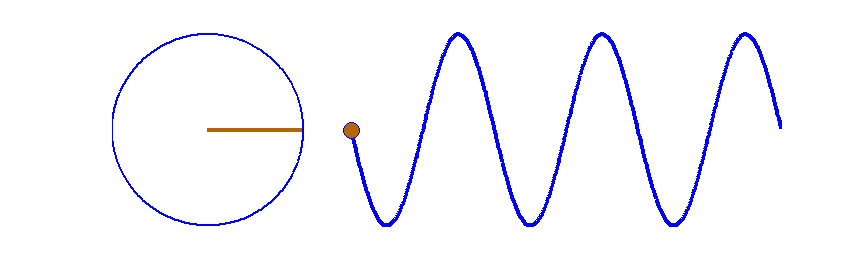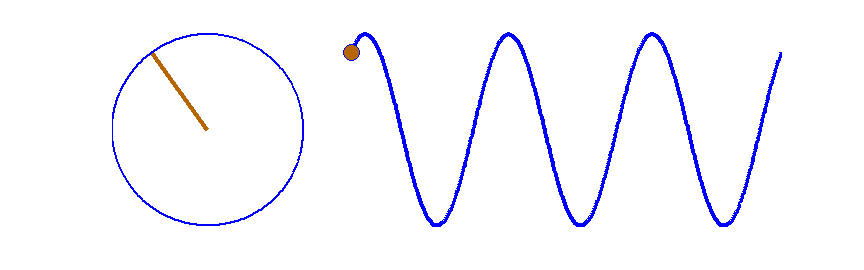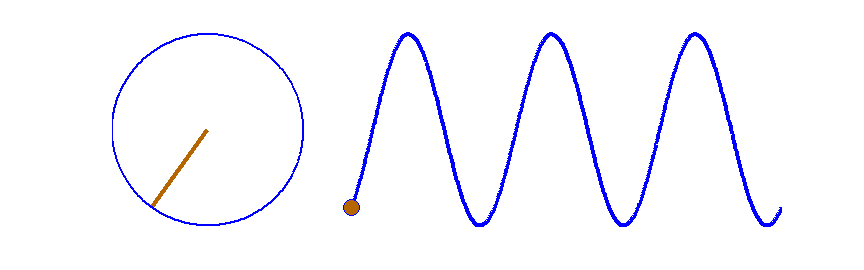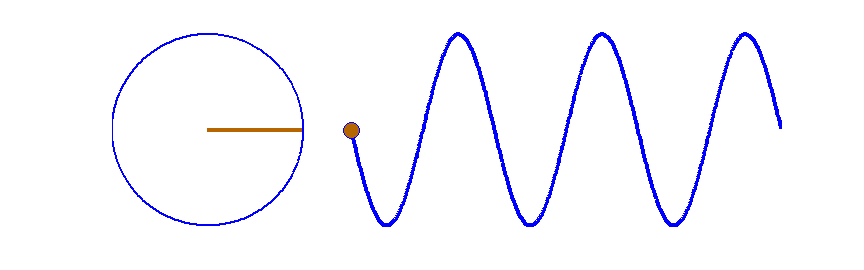
Векторная диаграмма представляет собой вектор, длина которого равна амплитуде колебаний, а угол φ между вектором и осью Оx – фазе колебаний. Так как фаза меняется с течением времени по закону φ(t) = ωt+φ₀, то вектор вращается вокруг точки O с угловой скоростью ω, равной круговой частоте гармонического колебания. При этом проекция вектора на ось Оx изменяется в соответствии с уравнением гармонических колебаний.

При гармонических колебаниях полная энергия системы (механическая энергия при механических колебаниях и энергия электромагнитного поля в электрическом колебательном контуре) с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

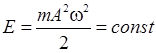 Гармонически колеблющаяся величина s(t) подчиняется дифференциальному уравнению:

,

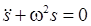которое называется дифференциальным уравнением гармонических колебаний.

Если какой-либо процесс описывается уравнением такого вида, то этот процесс представляет собой гармоническое колебаний с частотой ω.

Собственные колебания некоторых физических систем (например, пружинного маятника или электрического колебательного контура) при определенных условиях являются близкими к гармоническим. При этом частота собственных колебаний определяется физическими параметрами системы (например, массой груза и упругостью пружины для пружинного маятника). Значения амплитуды и начальной фазы зависят от начальных условий в системе.

Кроме того, гармоническими будут вынужденные колебания, если они происходят в результате гармонического внешнего воздействия на колебательную систему. Частота вынужденных гармонических колебаний равна частоте внешнего воздействия, а амплитуда и фаза зависят как от внешнего воздействия, так и от физических параметров колебательной системы (см. раздел 1.2.3).

Следует также отметить, что любое колебание (даже непериодическое) можно представить как сумму гармонических колебаний с различными амплитудами и частотами (разложить в ряд Фурье или интеграл Фурье (раздел 1.1). Зависимость амплитуд гармоник ряда или интеграла Фурье от частоты называется спектром колебательного процесса.

 < Предыдущая                     Оглавление                      Следующая >