Физические основы строительной акустики

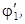
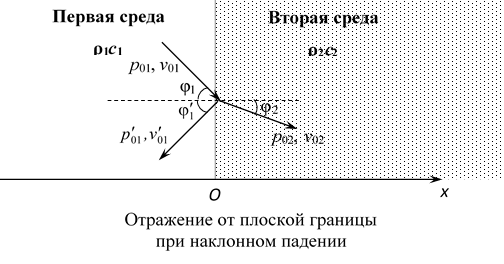
Рассмотрим случай наклонного падения плоской звуковой волны на границу раздела двух сред. Пусть угол падения равен φ₁, угол отражения  угол преломления φ₂ (см. рисунок).

 

  

 

Граничные условия в этом случае имеют тот же смысл, что и при нормальном падении: должны быть равны между собой нормальные к границе составляющие скорости и давления в первой и второй среде.

 Кроме того, должен выполняться закон Снеллиуса:

 

 

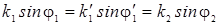
или, так как k = ω/c,

 

 

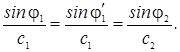
Этот закон универсален для всех типов плоских волн, падающих на плоские однородные препятствия. Физический смысл этого требования состоит в том, чтобы следы волн на поверхности раздела двух сред не обгоняли друг друга.

Следствием закона Снеллиуса являются законы отражения и преломления звука:

 

 

 

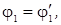
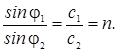
Величина n называется относительным показателем преломления звука.

Коэффициенты отражения и прохождения звуковой волны (по давлению) при наклонном падении имеют вид:

 

 

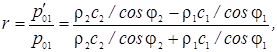
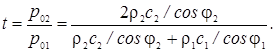
 Если обозначить  то формула коэффициента отражения примет вид:

 

 

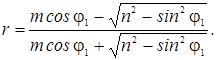
Проанализируем полученное выражение. При нормальном падении (φ₁ = 0) это выражение совпадает с формулой, полученной в предыдущем разделе. При скользящем падении (φ₁→ 90⁰) коэффициент отражения r → -1. При 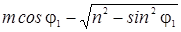 = 0 имеет место полное прохождение звуковой волны через границу (r = 0). Угол падения, при котором коэффициент отражения обращается в нуль, называется углом Брюстера:

 

 

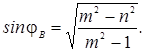
Для того, чтобы угол Брюстера был действительным, необходимо, чтобы выполнялось условие:

 

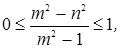
что, в свою очередь, реализуется либо при 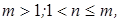 либо при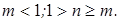

Если скорость звука в первой и второй среде одинакова (n = 1), то коэффициент отражения не зависит от угла падения:

 

.

 

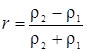Если скорость звука во второй среде гораздо меньше, чем в первой (c₂  <<  c₁), то 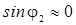 и, следовательно, φ₂ ≈ 0. Это означает, что независимо от угла падения звуковой волны на границу раздела, во второй среде волны распространяются только в направлении нормали к границе. Такой случай реализуется, например, при падении звуковой волны из воздуха на поверхность пористого звукопоглощающего материала. В этом случае коэффициент отражения при наклонном падении равен:

 

 

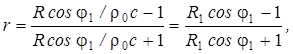
где R = ρ₂с₂ – волновое сопротивление материала, R₁ = R/ρ₀c - волновое сопротивление, выраженное в долях волнового сопротивления воздуха, или безразмерное волновое сопротивление (импеданс) материала.

Если импеданс границы, на которую падает звуковая волна из воздуха, комплексный:

                                    ,

 

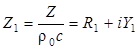коэффициент отражения также является комплексным числом: 

 

 

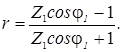
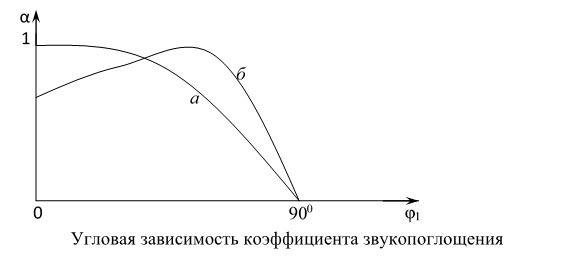
Коэффициент звукопоглощения при наклонном падении:

 

 

 Примерный вид угловой зависимости α представлен на рисунке.

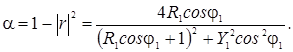
Кривая а соответствует R₁ → 1, Y₁ → 0, кривая б – другим значениям импеданса поверхности.

  

 

 

< Предыдущая                   Оглавление                    Следующая >