Физические основы строительной акустики

Пусть звуковая волна, распространяющаяся в среде с волновым сопротивлением ρ₁c₁, проходит через плоский слой материала с волновым сопротивлением ρ₂c₂ (см. рисунок). Толщину слоя обозначим d.  Такая ситуация реализуется, например, при прохождении звуковой волны через перегородку или перекрытие, изготовленные из однородного материала.

 

 

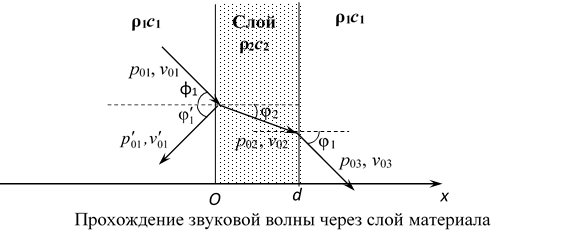
Используем те же граничные условия, что и в случае падения плоской звуковой волны на границу двух сред. Применив эти условия при x = 0 и при x = d, можно получить выражения для коэффициента отражения и коэффициента прохождения: 

 

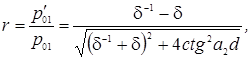
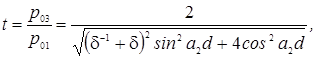
где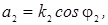   

 

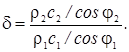
Проанализируем полученные формулы.

При δ = 1 (согласование волновых сопротивлений) получается, что r = 0, t = 1, то есть звуковая волна беспрепятственно проходит через слой.

 Кроме того, полное прохождение будет наблюдаться при 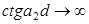, то есть пр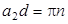и  или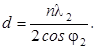

 

При этом на толщине слоя укладывается целое число полуволн (λ₂ = с₂/f  - длина звуковой волны в материале слоя).

Для тонкого по сравнению с длиной волны слоя (a₂d << 1) выражение можно упростить:

 

 

 

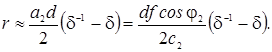
Таким образом, при заданном угле падения коэффициент отражения от тонкого слоя прямо пропорционален частоте звука.

При нормальном падении звуковой волны на слой коэффициент прохождения звука равен:

 

 

 

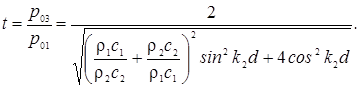
Для тонкого (по сравнению с длиной волны) слоя плотного материала (k₂d << 1, ρ₂c₂ >> ρ₁c₁)

 

 

 

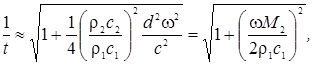
где M₂ = ρ₂d – масса 1 м² слоя (удельная масса слоя).

Величина, равная отношению интенсивности падающей волны к интенсивности прошедшей через слой волны, называется коэффициентом звукоизоляции: 

 

 

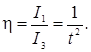
При нормальном падении коэффициент звукоизоляции равен: 

 

 

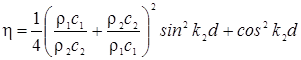
 При выполнении условий k₂d << 1 и  ρ₂c₂ >> ρ₁c₁

 

 

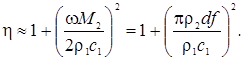
Из выражения видно, что коэффициент звукоизоляции возрастает при увеличении плотности материала и толщины слоя, а также при возрастании частоты звука.

На практике часто используется величина R_из(дБ), которая называется звукоизоляцией или индексом звукоизоляции слоя (перегородки, перекрытия и т.д.):

 

 

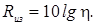
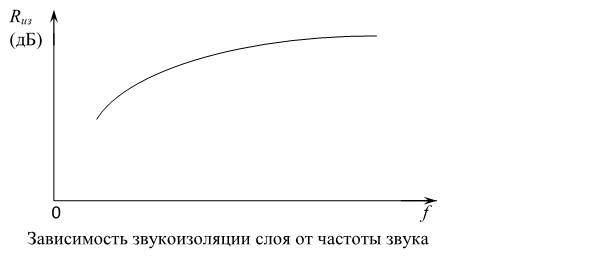
Эта величина показывает, на сколько децибел уменьшается уровень звука при прохождении через слой материала. Примерный вид частотной зависимости R_из(дБ) приведен на рисунке.

 

       Презентация к разделу 5

 

 

< Предыдущая                   Оглавление                    Следующая >