Физические основы строительной акустики

Комбинируя уравнение неразрывности, уравнение Эйлера и уравнение состояния, получаем уравнение для смещения частиц в звуковой волне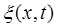

 

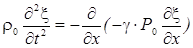
или

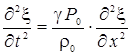
Если обозначить 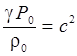, то

 

                                        

 

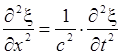
Таким образом, для ξ мы получили волновое уравнение (см. раздел 1.3 «Упругие волны в сплошной среде»), которое описывает волну, распространяющуюся в воздухе со скоростью, равной 

 

. 

 

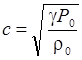Величина с называется скоростью звука.

При нормальных условиях плотность воздуха ρ₀ = 1,29 кг/м², атмосферное давление Р₀ = 1,013·10⁵ Па, и скорость звука в воздухе с = 330 м/с. При комнатной температуре (t = 18⁰C) с = 340 м/с.

Аналогичные волновые уравнения можно записать для звукового давления, акустических добавок к плотности и температуре.

Волны смещения, звукового давления, плотности и температуры распространяются с одинаковой скоростью.

Эти волны связаны между собой соотношениями: 

,

,

. 

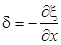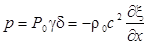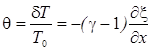Таким образом, если известно уравнение одной из этих волн, (например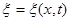), то остальные величины легко находятся.

Величина ρ₀с называется волновым сопротивлением среды.  При условиях, близких к нормальным, волновое сопротивление воздуха примерно равно

                                    

 

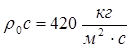
  < Предыдущая                   Оглавление                    Следующая >