2.4 Энергия звуковой волны. Уровень звука

 

Энергия звуковой волны. Интенсивность звука

 

Распространение звуковой волны сопровождается переносом энергии, которая зависит от звукового давления p и колебательной скорости v в каждой точке среды.

Средний поток звуковой энергии, проходящий в единицу времени через единицу поверхности, нормальной к направлению распространения волны, называется интенсивностью звука или силой звука (Вт/м2): 

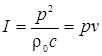image354.png. 

Векторная величина, характеризующая также направление переноса энергии в волне, называется вектором Умова: 

 

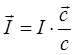image355.png. 

Наряду с интенсивностью звука используют величину плотность звуковой энергии 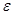image356.png(Дж/м3), равную энергии колебаний в единице объема звукового поля.

Можно показать, что в бегущей волне

 

 

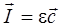image357.png. 

Таким образом: 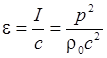         image358.png.

 

Передача энергии звуковой волны в область, ранее не затронутую волнами, требует непрерывного расходования энергии со стороны источника, возбуждающего звук. В тех зонах, где волна уже возникла, энергия непрерывно передается дальше со скоростью звука. Возникающие в среде переменные давления непрерывно совершают работу, ввиду чего и возникает волновое сопротивление (импеданс) 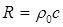image359.png при колебательных движениях частиц среды.

Формулы для силы звука: 

 

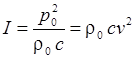
image360.png 

 

 подобны формулам закона Джоуля–Ленца для мощности электрического тока, только мощность, затрачиваемая при действии сил давления, расходуется не на выделение тепла, а на передачу энергии новым частям среды. Поэтому величину 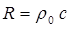image361.png часто называют также сопротивлением излучения среды.

 

 

Логарифмическая шкала силы звука. Децибелы

 

Отношение максимальной и минимальной интенсивности слышимого человеческим ухом звука очень велико и составляет 1014 раз (для звукового давления 107 раз). Поэтому для характеристики силы звука удобнее пользоваться логарифмическими величинами:

уровнем интенсивности звука, выраженным в децибелах (дБ):

 

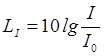
image362.png 

и уровнем звукового давления (дБ): 

 

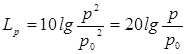image363.png,

 

где I0 и p0 – значения, соответствующие порогу слышимости на частоте 1000 Гц (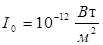image364.png, p0 = 2∙10-5 Па).

Значение p0 выбрано таким образом, чтобы при нормальных атмосферных условиях LI = Lp. Поэтому в дальнейшем будем использовать величину   L = LI  = Lp, которую называют уровнем звука в децибелах.

Уровень звука, соответствующий порогу слышимости на частоте 1000 Гц, равен 0 дБ. Болевой порог восприятия звука соответствует Iб = 102 Вт/м2 и рб = 2∙102 Па, что дает значение Lб = 140 дБ.

Введению логарифмических единиц измерения способствовало также то обстоятельство, что ухо человека реагирует не на абсолютное изменение интенсивности звука, а на относительное. Разница уровней в 1 дБ соответствует минимальной величине, различимой слухом, при этом интенсивность звука изменяется в 1,26 раза или на 26%. Если же разница уровней составляет 3 дБ, то сила звука изменяется уже в 2 раза.

 

Рассмотрим, как рассчитать суммарный уровень звука для звукового поля, создаваемого несколькими источниками. Возьмем для простоты два источника.

В любой точке пространства звуковое давление равно:

 

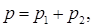
image365.png 

 

где р1 и р2 – мгновенные значения звуковых давлений, создаваемых в этой точке соответственно первым и вторым источником.

Результирующая интенсивность звука равна: 

 

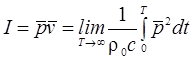
image366.png 

 

Если источники звука некогерентные, то есть создаваемые ими давления не связаны по фазе, то средний квадрат звукового давления 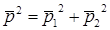  image369.png и, следовательно, 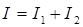image370.png  - интенсивность суммарного звукового поля равна сумме интенсивностей источников.

Таким образом, если поле создается N некогерентными источниками, то

 

I = I1+I2+…+IN ,     а 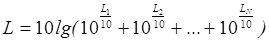     image371.png дБ, 

 

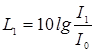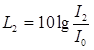где image372.png, image373.png … - уровни звука, создаваемые каждым

 

источником в расчетной точке.

При N одинаковых источниках шума, равноудаленных от расчетной точки, с уровнями звукового давления L0, суммарный уровень равен:

 

 

L = L0+10lgN.

 

Презентация к разделу 2

 

 

< Предыдущая                     Оглавление                      Следующая >