Физические основы строительной акустики

Звуковыми волнами (звуком) называется процесс распространения упругих колебаний малой амплитуды в сплошной среде. Область среды, в которой распространяются звуковые волны, называется звуковым полем. При распространении звуковых волн в газах и жидкостях смещение частиц среды происходят в направлении распространения волн. Такие волны называются продольными.

Теория звука в ее классической форме строится на основе законов движения жидкости и газа с учетом ряда особенностей колебательных движений с малой амплитудой.

Движение жидкости и газа подчиняется законам гидро- и аэродинамики. Так как для жидкости и газа они записываются в одинаковой математической форме, то мы будем говорить об уравнениях гидродинамики, подразумевая под жидкостью также и газ.

Уравнения гидродинамики в общей форме являются нелинейными и весьма трудно поддаются решению. Однако путем ряда предположений можно привести их к более простой форме.

Перечислим основные упрощающие предположения, справедливые для звуковых волн в воздухе:

а) пренебрегаем вязкостью и теплопроводностью воздуха;

б) считаем воздух однородной, изотропной, линейной средой;

в) предполагаем, что амплитуды колебаний давления, плотности и температуры звуковой волны малы;

г) процессы сжатия и расширения в звуковой волне считаем адиабатическими.

Введем ряд обозначений.

Пусть ρ₀ и Р₀ – плотность и давление воздуха в состоянии равновесия.

Тогда при распространении звука в среде общее давление в произвольной точке равно:

 

 

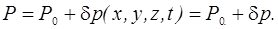
Величину δp, которая в звуковых процессах в газах обычно мала по сравнению с Р₀, будем обозначать далее через p = p(x, y, z, t) и называть звуковым давлением.

Соответственно для плотности:  

 

,

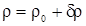где 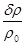<<1.

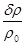 Величину  называют относительным изменением плотности.

Аналогично температуру среды можно представить в виде: 

 

Т = Т₀ + δТ (x, y, z, t)

где 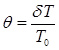<< 1 - относительная акустическая добавка к

 

температуре.

 

Видеофрагмент "Распространение звука" (1:53)

 

 

 

< Предыдущая                     Оглавление                      Следующая >