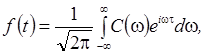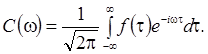Физические основы строительной акустики

Комплексные числа

 

Комплексными числами называются числа вида:

 

,

 

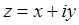где x и y – действительные числа, а i – мнимая единица (i² = -1).

 Числа x и y называются соответственно действительной и мнимой частью комплексного числа:

 

 

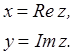
Число 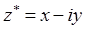 называется комплексно сопряженным числу z.

Комплексное число может быть представлено точкой на плоскости xОy:

 

 

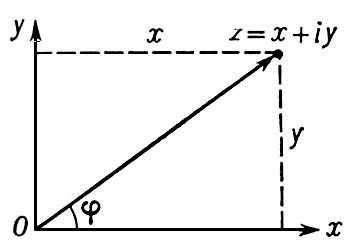
Длина радиус-вектора точки, изображающей комплексное число на плоскости xОy, называется модулем комплексного числа:

 

,

 

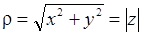а угол φ между радиус-вектором и осью Ox – аргументом комплексного числа:

 

.

 

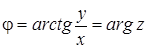Видно, что:

 

 

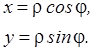
Тригонометрическая форма записи комплексного числа:

 

.

 

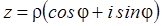В математике доказывается соотношение:

 

,

 

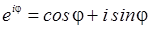
которое называется теоремой Эйлера.

Заменив φ на –φ, получим:

 

.

 

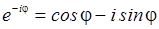Из теоремы Эйлера следует, что:

 

,

.

 

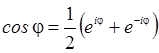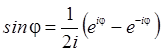Используя теорему Эйлера, комплексное число можно записать в показательной форме:

 

 

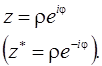
Основные операции с комплексными числами:

 

 

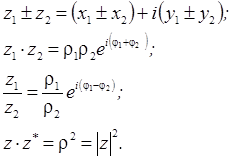
Ряд Фурье. Интеграл Фурье

 

Пусть f(t) – действительная периодическая функция с периодом T, для которой существует интеграл 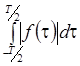. Тогда эту функцию можно представить в виде:

 

 

 

 

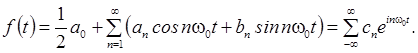
Такое представление называется разложением в ряд Фурье. Здесь:

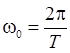-   - циклическая частота основного тона (первой гармоники);

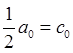-  - среднее значение f(t);

 

- члены ряда называются гармониками (n = 1 – первая гармоника или основной тон, n = 2, 3, … - обертоны).

Коэффициенты ряда определяются выражениями:

 

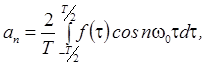
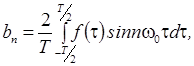
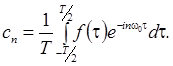
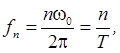 n-я гармоника имеет частоту  амплитуд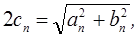у  фазу 

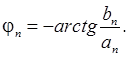
Если функция f(t) непериодическая, то ее можно представить в виде интеграла Фурье:

 

 

 

 

   < Предыдущая                     Оглавление                      Следующая >